On this web page you will find questions that will prepare you for Grade X Math exam for most countries. Practice as much as possible and attend my Q&A sessions based on a timetable that is sent to you. If you need to contact me please provide your contact information in the comments box below and I will reach out to you.

May your learning remove the darkness of ignorance from your life…. Rai Chowdhary
Gurukool students – Math classes start on May 3rd.
- If P(E) = 0, calculate P(not E)
- A student claims the probability of an event is -1/3; is this possible? Yes or No
- For a right angled triangle, if the hypotenuse = 10 cm., and the lengths of the sides are in the ratio 3:4, calculate the perimeter of the triangle.
- If a square is formed with the same area as the triangle in 3 above, what will be the length of it’s side?
- From a starting point A – I walk 5 km to the East then turn right and walk 3 km to the South. Then I turn right and walk 5 km again. How far am I from point A?
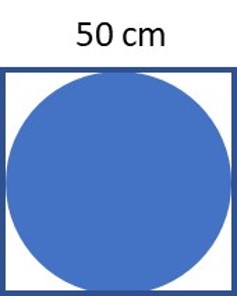
- Calculate the area of the four white shapes in the figure below given that the square has each side measuring 50 cm:
7. What is the perimeter of the shape shown below (a half circle attached to a square as shown):
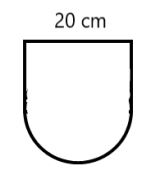
8. Calculate the area of the shape shown above
9. What will be the length of the side of an equilateral triangle if its area is the same size as the shape above?
10. What will be the radius of a sphere that has surface area of the same size as the shape above?
11. There are 5 male and 10 female fish in a tank; one is taken out at random. What is the probability that this fish will be a male?
12. In the following series, what will be the 29th. term?
3, 9, 15, 21….
13. In the above series, what will be sum of the first 10 terms?
14. At an electronics store, a TV regularly priced at R. 20,000 is discounted by 20%. Anil buys the TV at the discounted price, then sells it to a friend at 20% above the price he paid for it. Therefore his friend bought the TV at what price (select the correct answer from the ones listed below):
(a) R. 20,000 (b) R. 24,000 (c) R. 19,200 (d) none of the prices listed here
15. Calculate the probability of two die rolls resulting in a 2, then a 2 again if the same die is rolled twice.
16. While going upstream, a boat covers a distance of 24 km in 3 hours; while going downstream – it covers the same distance in 2 hours. What would be the speed of the boat in still water, and what is the speed of the water flow?
17. Find two numbers whose sum is 30 and product is -216
18. The product of Ahmed’s age two years ago and two years from now is equal to three times his age now. What is Ahmed’s age now?
19. Which of the following correctly define Cot A?
(a) 1 / Tan A (b) Cos A / Sin A (c) (Sin2A + Cos2A) / Tan A (d) All three
20. The trigonometric identity Sec2A = 1 + Tan2A is true for which type of triangle?
(a) Equilateral (b) Isosceles (c) Obtuse (d) Any of a, b, or c (e) None of these
21. For the shape shown below, what is the perimeter of the four white areas in this diagram?

22. If the area of the four white spaces in the diagram above is used to create an equilateral triangle, what will be it’s area?
23. For the triangle in Que 22 what will be the length of its side?
24. If the four white spaces in the above diagram are used to create an Isosceles right angled triangle, what will be the length of it’s hypotenuse?
25. What is the probability that you will get a prime number when a die is rolled once?
26. Answer as true or false:
(a) An altitude of a triangle will always bisect the angle at the apex
(b) An obtuse angled triangle cannot be an Isosceles triangle
(c) A right angled triangle can also be an obtuse triangle
(d) For a right angled triangle, angle ABC is 60o, therefore, the ratio of sides AC:BC will be 2:1
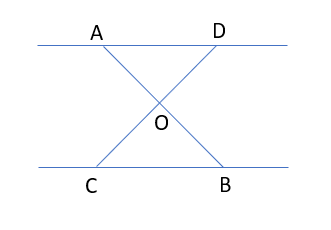
27. For the diagram shown below, calculate angle AOC if angle OAD and ADO are 60o each
28. For the diagram above, what will be the length of AD if the vertical distance between the two horizontal lines is 20 cm.
29. A plane leaves from Point A and flies 300 km North, then turns left by 60o and flies another 100 km. What is the distance of the plane now from the starting point?
30. If the roots of the equation 9x2 – kx + 1 = 0 are equal, what is the value of k?
31. Two cubes, one of side 4 cm and the other of side 5 cm are melted and combined to make a sphere. What will be the surface area of this sphere?
32. Find the HCF and LCM of 14 and 49
33. Find the roots of the polynomial x2 – 4
34. The series shown below has 20 numbers; find the sum of the last four.
-2, -6, -10…
35. The 12th. term of the Arithmetic Progression -4, -1.5, 1… is which of the following?
a) -12 b) 633 c) -28 d) none of these
36. From a point A, the length of a tangent to a circle is 4 cm, and the distance from A to the center of the circle is 5 cm. What is the diameter of the circle?
37. Which of the following is true?
a) The shortest line drawn inside a circle is the diameter
b) The longest line drawn inside a circle is the radius
c) The longest line drawn inside a circle is the diameter
d) The longest line drawn inside the circle is a tangent
38. Identify the quadrants where the following points will lie:
a) -3, -2 b) 1, -6 c) 1, 9 d) -3, 2
39. For the above calculate the distance between the point b and c
40. If Sin A = 3/5, what will be Cos A?
41. If the surface area of a hemisphere is 49 cm2 what will be the volume of that sphere?
42. Which of the following are rational numbers and why?
a) 1/2 b) 1/root(2) c) 3/2 d) 0
43. A vertical palm tree 12 m tall casts a shadow that is 20 m long. The pole nearby casts a shadow 24 m long. What is the height of the pole?
44. Calculate the value of: (Cos260 – Tan245 + Cosec230) / (Sin30 + Cos60)
45. Calculate the area of the blue region in the figure below if ABCD is a square of side 10 cm and BCE is a semicircle with BC as its diameter.
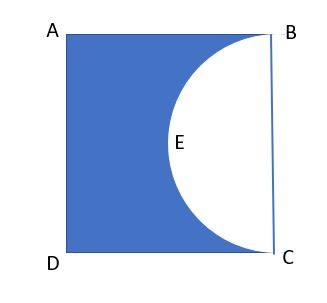
46. For the figure above, which of the following are true?
a) The diagonal AC will be equal to the diameter of the semicircle
b) The perimeter of the semicircle will be equal to half of the perimeter BADC
c) AC2 = BC2 + AB2
47. Find the 10th term in the series below:
-7, -3 1/2, 0, 3 1/2 ….
48. Calculate the distance between points (3, 1) and (-2, 7)
49. The perimeter of a circle is 31.4 cm, what is the area of one of its quadrants?
50. A box contains five red, four white, and 11 blue balls. If a ball is drawn at random what is the probability it will be red.
51. For the above situation, what will be the probability it will be neither blue, nor white.
52. A cylindrical bucket of diameter 45 cm and 60 cm high is filled with sand. Then it is emptied on the ground and a conical pile is created; its height measures 30 cm. What will be the diameter of the base, and what will be the slant height of this pile of sand?
53. A class of 20 students scores as below in their Geography exam:
45, 44, 59, 90, 78 88, 89, 34, 28, 66 44, 55, 93, 49, 81 55, 85, 44, 76, 44
Calculate the Mean, Median, and Mode for the above data
54. Arrange the data in above question using class intervals of width 5 and display it in a table
55. Answer the following as true / false:
(a) Experimental probability is the same as theoretical probability
(b) If two figures are congruent, they must also be similar
(c) In the figure below, triangles AED and BCD are similar
(d) In the figure below, angle A will be equal to angle D
(e) A radius of a circle touches a tangent at point A; therefore angle A must be an acute angle
(f) Tangents drawn at the ends of the diameter of a circle will be parallel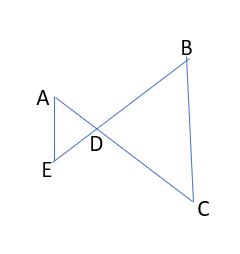
56. The radii of two circles is 10 cm and 20 cm; what will be the circumference of a circle formed by the combined area of these two circles
57. A 30o sector of a circle is colored blue; rest of the circle is white. What is the area of the white portion?
58. Re-write the equation of motion v = ut + (1/2)(at2) to determine a. (Hint: the equation should have a on the left side such that a = …. )
59. At present Mukesh is four years younger than Abida. If Abida is “n” years old, what will be the sum of their ages three years from now?
60. Calculate the slope of the line passing through (3, -4) and (5, 8)
61. In the graph shown below, calculate the speed of each boat.
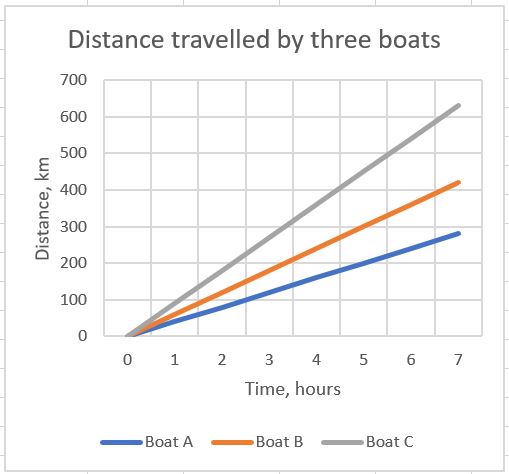
62. In the graph above, how much ahead is Boat C from Boat A at 4 hours?
63. The vertices (corners) of a rectangle lie at (2, 2), (2, 4), (-2, 4), and (-2, 2); calculate its perimeter and its area
64. A square has its diagonally opposite vertices (corners) at (2, 2) and (-2, -2). What is its area and its perimeter?
65. Which of the following is an AP? Find the next three terms for that…
(a) 2, 0, -1, … (b) 3, 9, 81, …. (c) 9, 5, 1, … (d) 12, 19, 26, …
66. Factorize the quadratic and find it’s roots: 2x2 + 9x + 7
67. For an AP, a = 11, and the 6th. term is 21. What will be the 10th. term?
68. Two die are thrown at the same time (one is red the other is blue). What is the probability that the difference of the numbers appearing on their faces will be equal to 3?
69. A triangle ABC drawn inside a semi-circle has the diameter of 20 cm. as its base. If it is an isosceles triangle and its apex A lies on the circle, what will be the area of the triangle?
70. For the figure below, AB and AD are tangents to the circle; what will be the length of AB if AD = 16 cm, and AC is the bisector to angle BAD. 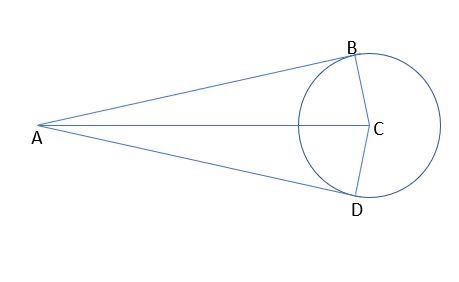
71. In the figure above, if the radius to the circle is 5 cm. what will be the area of the figure ABCDA?
72. Which term of the following series is -27?
63, 60, 57, …
73. For the figure shown below – what will be the area of the dark blue region (a quadrant) if the diameters of the outer and inner circles are 30 cm and 15 cm?

74. For the figure above what will be the perimeter of the dark blue region. The outer circle is 30 cm and the inner circle is 15 cm in diameter; the arc is 90o.
75. How many two digit numbers are divisible by 5?
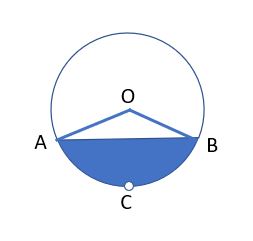
76. One card is drawn from a deck of well shuffled cards. What is the probability it will be:
(a) an ace
(b) a card with hearts
(c) a queen or a king
(d) a card with number 2, 3, or 4
77. What will be the probability of a coin that is tossed falls in the blue space shown in problem 73. The circles have diameters of 30 and 15 cm., and the arc is 90o
78. Using the data from question 53, create groups of class interval 5 and a frequency table. Then calculate the Mean, Median, and Mode for the grouped data.
79. Plot the lines x + 3y = 7, and 2x – 2y = 12. What are the coordinates of the point where they intersect? Calculate the slope for each line.
80. Will the number 96 occur in the series 4, 7, 10… ? If so, where will you find it?
81. Answer the following as true or false:
(a) The equation to a parabola will have a degree of one
(b) A linear polynomial ax + b will have exactly one zero (as long as a is not equal to 0)
(c) For a polynomial ax2 + bx + c, the product of zeroes will be = c / a
(d) The lines with equations 3x + 6y – 18 = 0, and x + 2y – 3 = 0 have the same slope
(e) For the equations of (d) above, the y intercepts are -18, and -3
82. A farmer has a rectangular plot of land with an area of 12,800 sq. meters. If the length of the plot is twice the width, and he wants to build a fence around the plot, how long would it be?
83. Solve the equation by factorization: 3x2 – 7x + 4 = 0
84. Solve the above equation by using the quadratic formula
85. The shadow of a tower standing on level ground is 20 meters longer when the sun’s altitude is at 30o than when the sun is at an altitude of 60o. Calculate the height of the tower.
86. For the figure below, what are the coordinates for A and B? What will be the length of line AB? (Also verify your calculation using Excel, or a calculator)
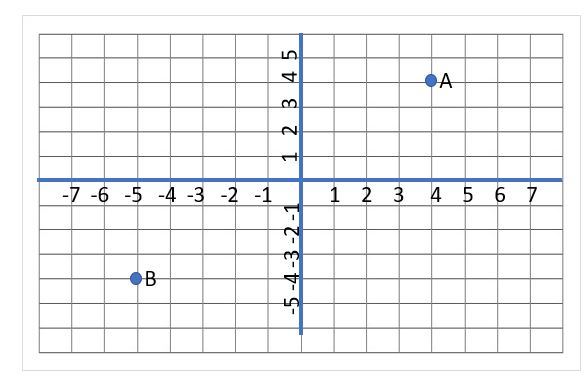
87. What will be the equation for the line AB in the above figure?
88. A cylinder of height 60 cm and diameter 10 cm is melted to form a hemisphere. What will be the ratio of the surface areas of the cylinder and the hemisphere?
89. Select the correct answer from the following
The shape in red below is a
(a) Parabola with zero at (1, -4)
(b) A hemisphere
(c) Parabola with zeroes at -1 and 3
(d) None of the above
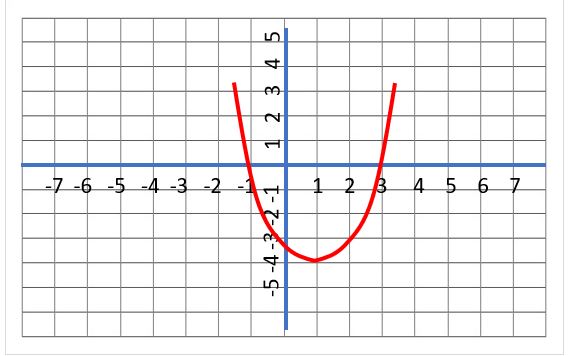
90. Select the correct answer from the following
For the red line in the figure above:
(a) The equation will have a degree of 1
(b) There is no y intercept
(c) The vertex is at (1, – 4)
(d) There is no symmetry
91. Answer each of the following as true or false:
(a) A triangle inscribed in a circle with the diameter as its base and the apex on the circumference can have one obtuse angle
(b) The longest chord in a circle is it’s diameter
(c) It is possible for a circle’s area to be equal to its circumference (what will be the radius in this case?)
(d) It is not possible for a sphere’s surface area to be equal to it’s volume (for any value of r)
92. Select the correct answer from the following choices
The number 1008 can be expressed as a product of primes by:
(a) 72 x 32 x 24 (b) 7 x 32 x 24 (c) 72 x 32 x 22 (d) 14 x 32 x 234
93. The apex A of a triangle is at (5, 5); the other corners (B and C) are at (2, 0) and (8, 0). A bisector is drawn from the apex A. What will be the coordinates of the point where the bisector touches the base BC?
94. What will be the coordinates of the point P that divides a line segment with end points at (5, 0) and (0, 5) in the ratio of 1:4?
95. Triangle ABC is a right angled isosceles triangle with A being the right angle. Find the value of SinB
96. Conduct a web search to find the following (you must show pictures of the web page):
(a) Equation for a circle
(b) Formula to calculate area of parallelogram using a side and the height
(c) Formula for volume of the frustum of a right circular cone
(d) Slope intercept equation for a line
(e) Formula for area of segment of circle
(f) Section formula for line
97. Conduct a web search to find the acceleration of Maruti Swift, then calculate the velocity of the car 6 seconds after starting from 0.
98. Find the formula for calculating the mode of grouped data then answer question 5 on page 276 in your book (Chapter 14)
NOTE: This problem is for students using the NCERT Math Text book for Class X students
99. For a circle, the center is located at -3, -2. What will be the equation to the circle if the radius is 5 cm? Show the circle on a graph also.
100. Find the sum of the 10th., 11th., and 12th. terms of the progression 10, 15, 20….
101. The product of two consecutive integers is 272, what are the integers?
102. Calculate Cot60 – Sin60 – Cos60 + Tan 60
103. What will be the angle between the hour hand and minute hand when the time is six ‘o clock
104. The sum of areas of two squares is 34 sq. cm; if one square’s side is 2 cm longer than the the other, what are sides of each square?
105. Write all the trigonometric identities for a right angled triangle
106. For the diagram below, what will be the ratio of areas of orange circle and the white space? The diameter of each of the three circles is 10, 20, and 30 cm.

107. For the diagram above, what will be the difference in areas of the blue and white spaces? The diameters of the three circles is 10, 20, and 30 cm.
108. For the diagram below, what will be the areas of the triangle and the blue area? The angle at the apex of the triangle is 120o and the radius is 7 cm.
109. For the diagram above, what is the perimeter of the area bound by OACBO
110. A plane takes off from the runway at 12:05 PM with a velocity of 300 km / hr. It climbs at an angle of 30o with constant velocity; what will be the time when the plane reaches a height of 5 km. from the ground?
111. Write a quadratic polynomial the sum of whose zeroes is 8 and and product of zeroes is -9.
112. Create a graph of the polynomial for question 111 and find the zeroes from the graph
113. Divide x3 + x2 – x – 1 by x – 1
114. In the diagram below, if angle A = 50o and C is 70o what will be angle FEA given that EF is perpendicular to the base?
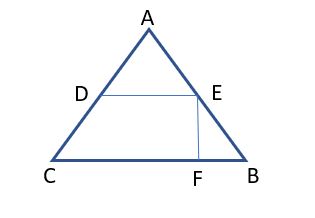
115. In the diagram above, AD is 5 cm, and DC is 10 cm. If DE is parallel to the base, what will be the ratio of AB to AE?
116. Solve: x2/24 – x/9 – 1/8 = 0
117. If CotA = 4/3, calculate (1 – SinA)(1 + SinA) / (1 – CosA)(1 + CosA)
118. Find angle A for each of the following:
(a) TanA = 0
(b) TanA = 1
(c) TanA = not defined
119. Prove (TanA + SinA) / (TanA – SinA) = (SecA + 1) / (SecA – 1)
120. Solve algebraically: 2x + 3y = 11, and x – 2y = – 12
121. Solve the following:
(a) (2/sqroot3) x (6.sqroot3) + 9.sqroot2/sqroot3 – 1/sqroot27
(b) 24/sqroot2 – sqroot27/32 + 43/sqroot32
(c) (a+b)3 – (a+b)2 – (a+b)
122. A cone holds 2 kg. of water. If the vertical height of the cone is 20 cm, what will be the radius of the cone?
123. Find the 15th term of a series if the 3rd term is 12 and the 6th. term is 30
124. Solve the pair of equations given below:
x + y = 6
-3x + y = 2
125. Create graphs for both equations of question 124 and find the coordinates of their intersection point.
126. A solid hemisphere of diameter 14 cm. is melted to form a cone of height 20 cm. What will be its slant height?
127. A bicycle wheel has a diameter of 42 cm. If it rotates 5 times, what will be the distance covered by the bicycle?
128. A truck has a wheel of diameter 120 cm. If the truck is moving at 20 km / hour, how many revolutions will the wheel make in 5 minutes?
129. A ball has a diameter of 14 cm. If the ball rolls on the ground making 20 revolutions, will it reach a goal which is 20 meters away? How far will it go?
130. A ball has a diameter of 28 cm. and it is at point A on the ground. The goal is 25 meters from point A. How many revolutions of the ball are needed for it to reach the goal?
131. Solve the equations 2x + 3y = 9, and x – y = 3 by the substitution method. Use this link to see the solutions:
https://byjus.com/maths/solving-linear-equations/
132. Solve the equations 2x – 3y = 7, and 3x + 6y = 21 by the substitution method.
133. Solve the equations in 132 by the graphical method. Use the link of question 131 to learn the graphical method or read it in your book
134. Anand has to walk 3.96 km every day. He walks around a park of diameter 42 m. How many times should he go around the park?
135. Solve equations 2x + 3y = 28 and 3x + 9y = 78 using the substitution method
136. Solve the above equations of using the graphical method
137. The product of two consecutive integers is 210, find the integers
138. A box contains 30 balls with numbers 1 to 30. If a ball is drawn at random, what is the probability that the ball will have a number divisible by 5?
139. Solve equations 2y – 3x = -2, and y – 2x = 1 by the cross multiplication method
140. Solve the equations in question 139 by substitution method
141. Solve the equations in question 139 by the elimination method
142. If the roots of the quadratic equation 3x2 + kx + 3 are equal then what is the value of k?
143. If the vertices of a rectangle are: (2,2), (2,4), (x,2), (6,4) what is the value of x?
144. If the vertices of a parallelogram are: (6,1), (8,2), (9,4), (p,3) then what is the value of p?
145. If the vertices of a triangle are: (1,2), (1,6), (4,2) what is the length of the longest side?
146. Find two consecutive odd numbers who’s difference of squares is 40
147. In a fraction when 1 is added to the numerator, it reduces to 1; if 1 is added to the numerator and 1 is subtracted from the denominator it reduces to 2. What is the fraction?
148.
(Click here to learn how to Solve Math word problems –
Example 1
Example 2